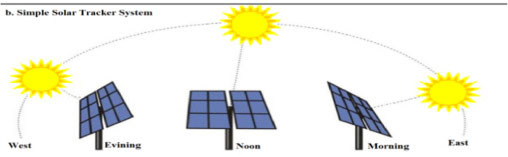
Solar tracking is an essential component of solar panel systems, and one commonly used algorithm for tracking is the astronomical algorithm. But what exactly is the astronomical algorithm and how does it accurately calculate the azimuth and altitude of the sun? In this article, we will explore the concept of astronomical algorithms and their significance in precise solar tracking.

What are Astronomical Algorithms?

Astronomical algorithms refer to a series of calculations aimed at observing and measuring the positions of celestial bodies, exploring their motion patterns, and studying their physical properties, chemical composition, internal structure, energy sources, and evolutionary patterns. These algorithms utilize principles of Euclidean geometry, mechanics, relativity, spectroscopy, and other scientific theories to derive and compute a comprehensive understanding of celestial bodies.

Historical Background:

The earliest known Chinese literature on astronomical algorithms can be found in the book “Siku Quanshu,” specifically in Volume 106, which describes the principles behind celestial motion. These ancient texts laid the foundation for modern astronomical algorithms.

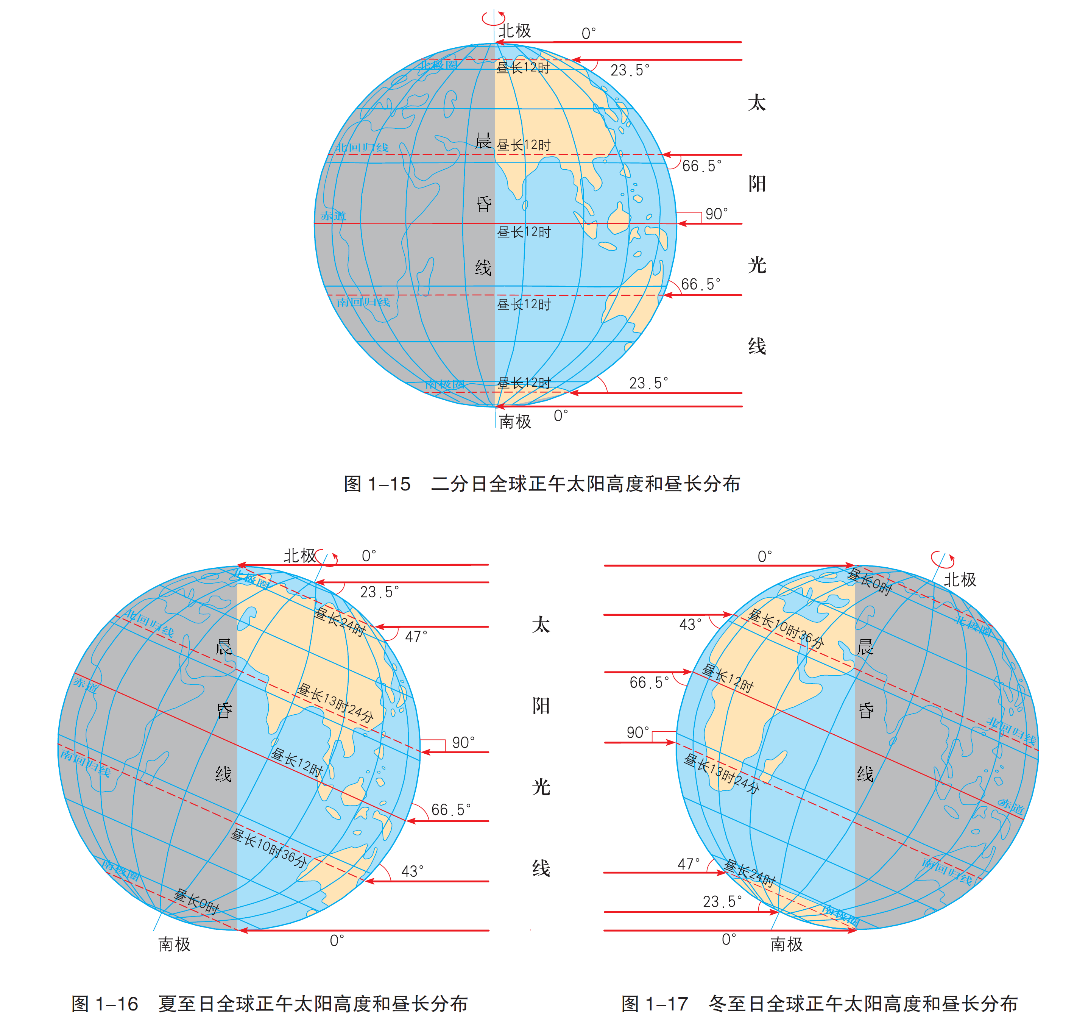
Calculating Solar Azimuth Angle:

For solar tracking systems, the astronomical algorithm utilizes the formula for calculating the solar azimuth angle. The formula is as follows:

Azimuth (A) = cos^-1((sin(ϕ)sin(δ) – sin(ϕ)) / (cos(H)cos(ϕ)))

In this formula:

– H represents the solar altitude angle.

– A represents the solar azimuth angle.

– ϕ represents the latitude of the system’s location.

– δ represents the solar declination.

– t represents the hour angle.

By utilizing this formula, we can determine the precise solar azimuth angle at any given time and location on Earth. It’s important to note that the calculation of the solar azimuth angle relies on two key concepts:

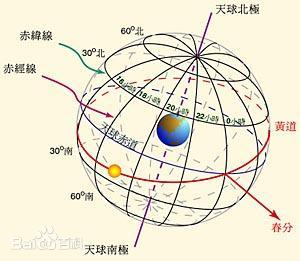
Celestial Sphere Model:

The calculation of the azimuth angle assumes that the sun and all celestial bodies are placed on a sphere with the same center as the Earth, sharing a common rotation axis and an infinitely large radius. This simplification allows astronomers to represent the positions of celestial bodies and analyze their relationships using great arcs on the celestial sphere. For example, the sun’s apparent motion on the celestial sphere is approximately 1 degree per day and completes a full circle (360 degrees) in one year, known as the sun’s annual apparent motion along the ecliptic.

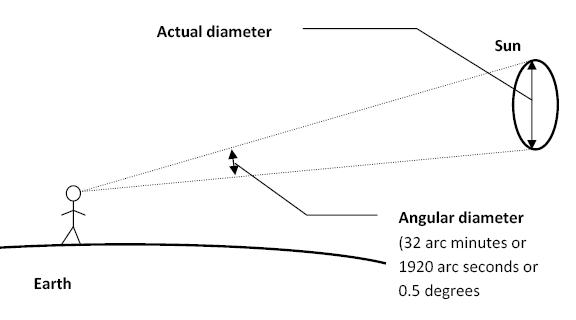
Approximation of Parallel Light:

Despite the spherical shape of the sun and its emission of light in all directions, its radius (6.955×105 km) in relation to the Earth’s radius (6371 km) is negligible compared to the distance between the sun and the Earth (1.5×108 km). As a result, the solar rays can be approximated as parallel when they reach the Earth’s surface.

However, it’s important to consider that the sunlight experiences refraction and scattering when passing through the atmosphere.

Refraction causes a slight deviation in the direction of light, while scattering splits the direct solar light into different scattered lights, including Rayleigh scattering, Mie scattering, and Raman scattering. These combined scattering mechanisms give the sky its blue color and create diffuse illumination even in shaded areas.

Optimizing Solar Tracking:

Although the astronomical algorithm provides a solid foundation for solar tracking, it does not account for the effects of atmospheric conditions and terrains. The presence of scattering light due to atmospheric conditions can affect the effectiveness of solar tracking in areas with low direct sunlight.

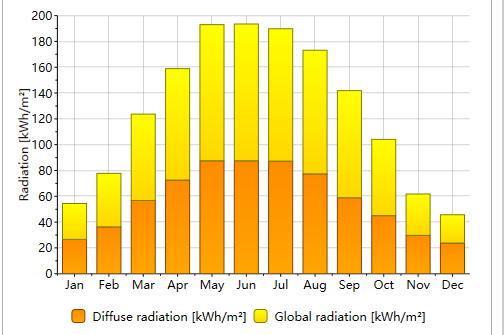
▲High direct light ratio area

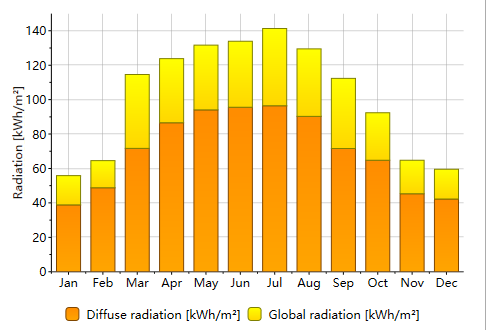
▲Low direct light ratio area

To address this, Mokun has developed an intelligent tracking algorithm that considers the total irradiance and scattered irradiance around the solar tracking system. By analyzing the ratio of total irradiance, direct irradiance, and scattered irradiance, the tracking algorithm can dynamically adjust the tracking strategy. This optimization is achieved through a combination of astronomical algorithms, diffuse light tracking, and cloud-tracking strategies, enabling maximum solar energy generation for photovoltaic systems.

Conclusion:

In conclusion, the “astronomical algorithm” that guides solar tracking is based on the celestial sphere model and the calculation of solar azimuth angles. However, to account for atmospheric conditions and terrains, continuous optimization based on the astronomical algorithm is necessary to achieve more precise and effective solar tracking. By combining astronomical algorithms with real-time data analysis, we can fully leverage the potential of solar tracking systems to maximize solar panel efficiency and generate reliable renewable energy.

Keywords: Mokun solar tracker, solar energy innovation, solar panel efficiency, future-ready solar solutions, renewable energy advancement, reliable solar tracking, Mokun MK-TSS tracker, solar power optimization, 14 years of innovation